Chaos and Chaotic Attractors¶

Where do I find chaotic attractors?: Chaotic attractors are the solution of mathematical systems: differential equations systems (eg. Lorenz system), time-delay systems (eg. Mackey-Glass system), discrete-time dynamical systems (eg. Hénon map), fractional-order systems, etc. These systems are models for physical, chemical, mechanical or electrical phenomenons.

Rössler attractor¶

For the parameters $a=0.398$ , $b=2$ and $c=4$ , the Rössler system [ROS76]

$\left\{\begin{aligned} \dot{x} &= -y -z \\ \dot{y} &= x +ay \\ \dot{z} &= b+z(x-c) \end{aligned}\right.$

have a chaotic attractor as solution (Fig. 1).

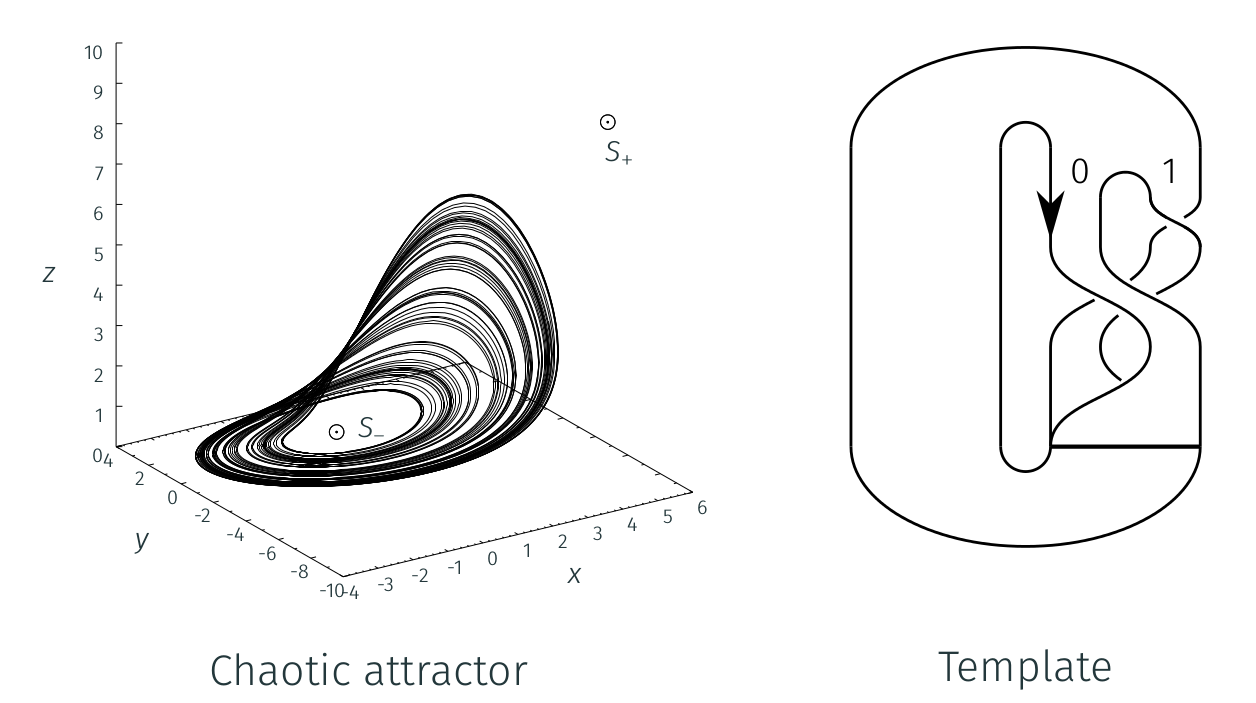
_images/rossler_01_trans.png — Fig. 1 - Rössler attractor (left) and its template (right).¶

This attractor is described by a template obtained with topological characterization method (see [LET95] where the method is applied to this attractor). This method uses orbits properties to detail the attractor structure. The orbits in the phase space have the same linking numbers in the attractor template. Fig. 2 displays two orbits: a period-1 and a period-2 orbits with the same linking number equal to -1.

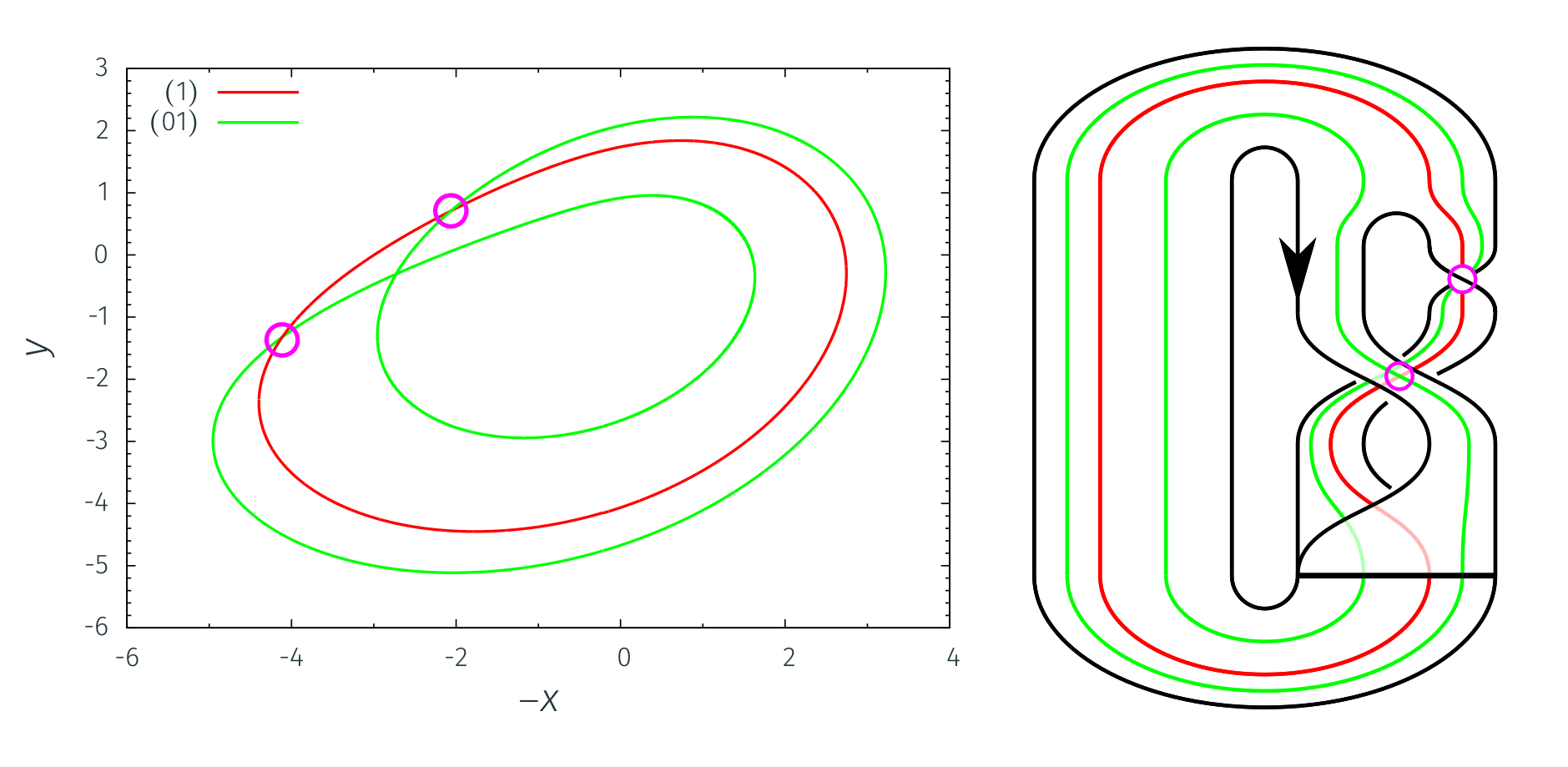
_images/accueil_transparent.png — Fig. 2 - Period-1 and period-2 orbits in the phase space (left) and in the template (right) (negative crossings are highlighted).¶

The template of this attractor is described by the following linking matrix:

$\left.\left[ \begin{array}{cc} 0 & -1 \\ -1 & -1 \end{array} \right]\!\!\right] .$

I define conventions to ensure that a template correspond to a unique linking matrix. I establish the topology of eight attractors solution to the Rössler system.

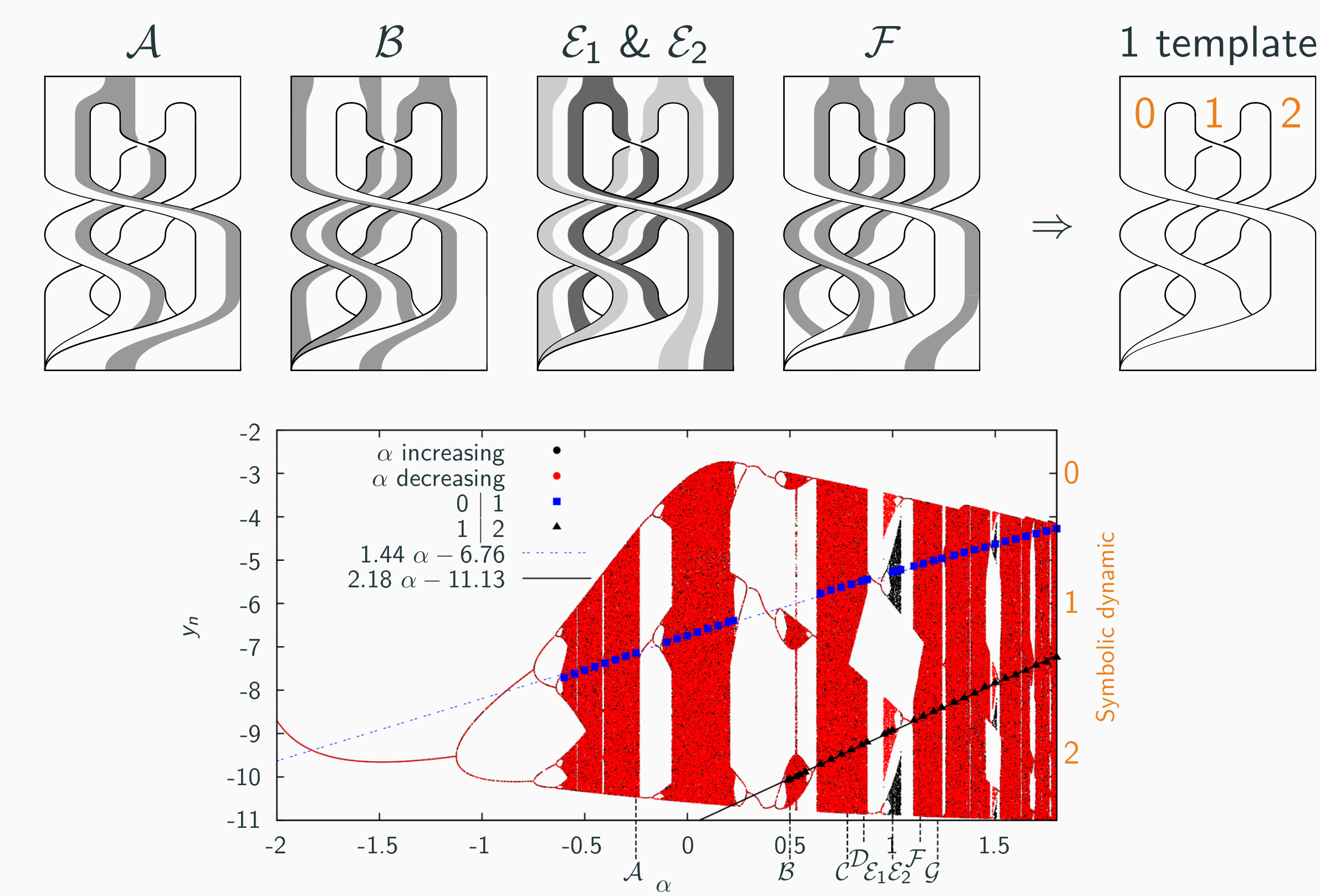
_images/subtemplate.png — Fig. 3 - Eight templates are subtemplate of one unique template.¶

In the parameter space, these attractors comes from the same bifurcation diagram and are subtemplates of a template described by

$\left.\left[ \begin{array}{ccc} 0 & -1 & -1\\ -1 & -1 & -1 \\ -1 & -1 & 0 \\ \end{array} \right]\!\!\right] .$

Foliated templates¶

I work on foliated attractors solution of Lorenz and Chen systems. I establish their templates using periodic orbits in order to details the common structure: the foliation. Fig. 4 is the template of the Chen attractor [CHE99].

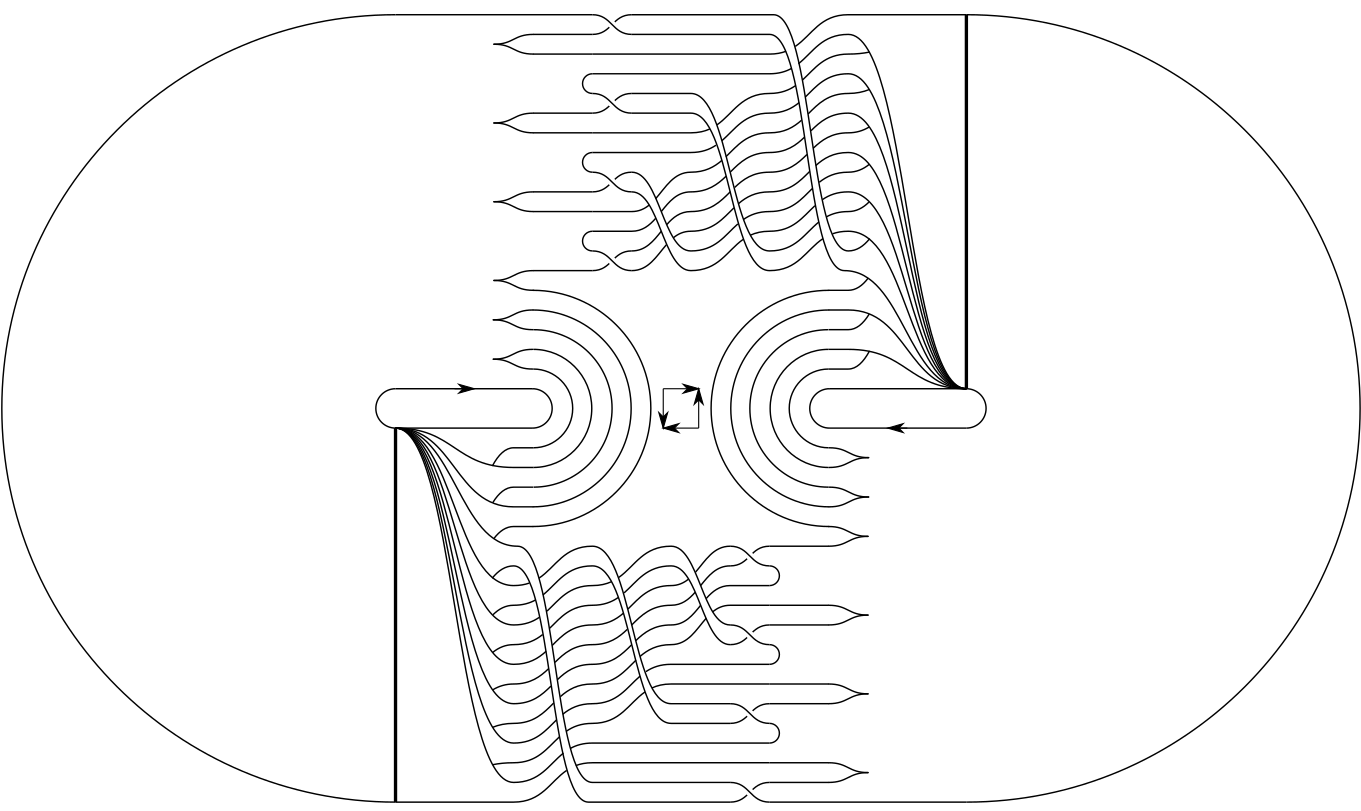
_images/chen_01_template_trans.png — Fig. 4 - Template of the Chen attractor.¶

This template is foliated with the same schema repeated for than three times. The Lorenz system can exhibit similar behavior with only two repetition of this foliated structure.

Concatenation¶

The second part of my studies is dedicated to the analysis of these templates described with linking matrices. The purpose is to propose algebraic tools to work with templates in order to build, compare and validate them. For instance, concatenation of linking matrices is a tool that can be used to obtain the template of a symmetric attractor.

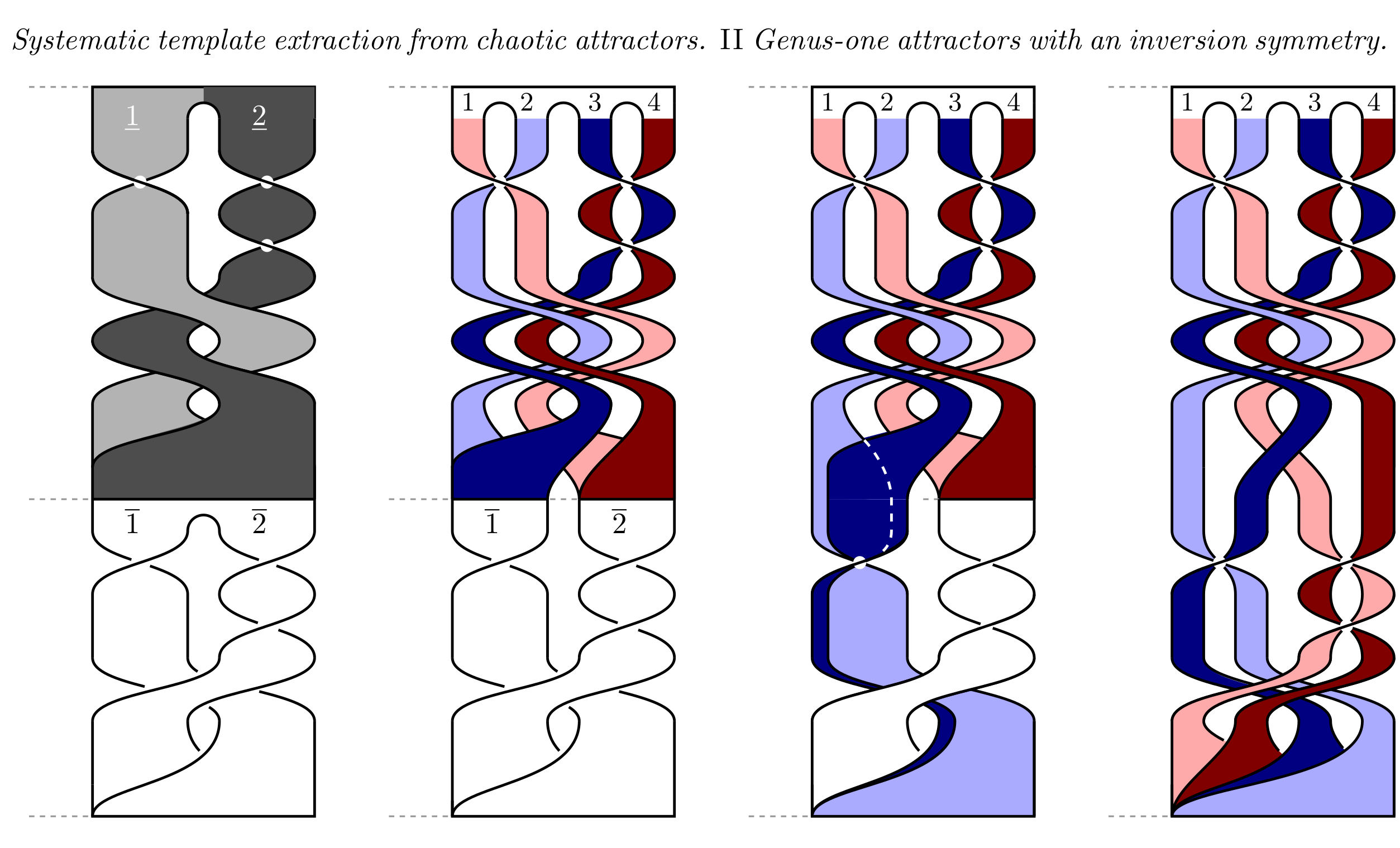
_images/concat.png — Fig. 5 - Concatenation: a step by step illustration of Fig. 10 and Eq. 25 of [ROS15].¶

The following concatenation is illustrated by Figs. 5 and 6

$\left.\left[ \begin{array}{cc} -1 & -2 \\ -2 & -2 \\ \end{array} \right]\!\!\right] + \left.\left[ \begin{array}{cc} 1 & 1 \\ 1 & 2 \end{array} \right]\!\!\right] = \left.\left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 0 & -1 & -1 \\ 0 & -1 & -1 & -1 \\ 0 & -1 & -1 & 0 \end{array} \right]\!\!\right].$

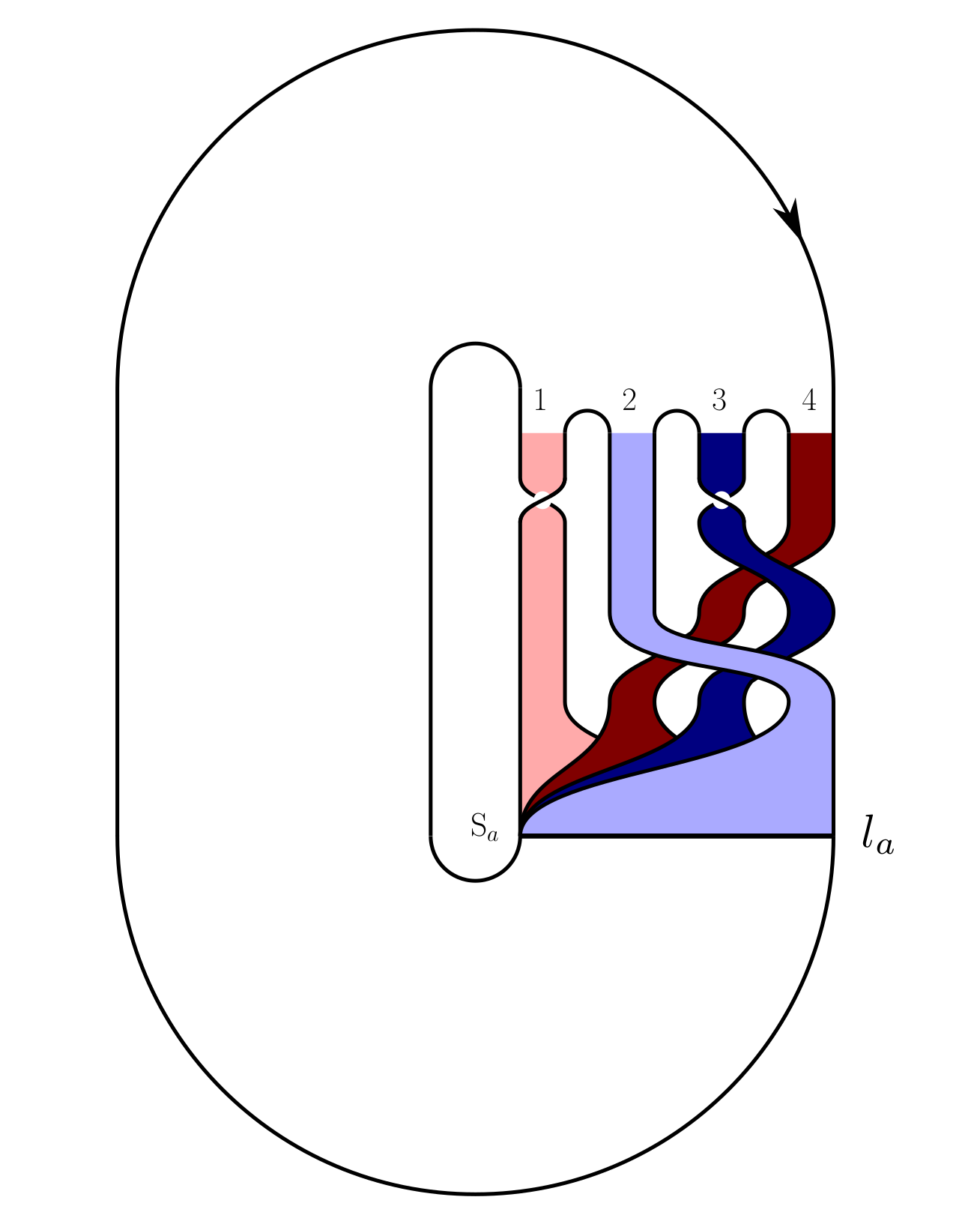
_images/concat_result.png — Fig. 6 - Template resulting of the concatenation.¶

CATE tool to visualize template¶

We consider templates of chaotic attractors bounded by a genus-1 torus described by a linking matrix. We provide a novel and unique tool to validate a linking matrix, to optimize the compactness of the corresponding template and to draw this template. Finally, the drawing process of the template corresponding to the matrix is saved in a Scalable Vector Graphics (SVG) file. CATE (Chaotic Attractor TEmplate) is a tool available online: gitlab.uni.lu or PyPI

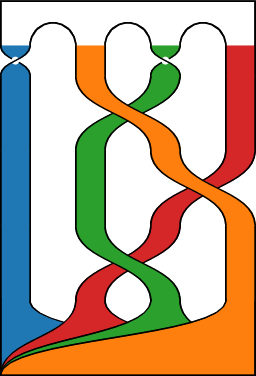
_images/cate.png — Fig. 7 - Template of Fig. 6 made with `cate`.¶

References

ROS76: O.E. Rössler, An equation for continuous chaos, Physics Letters A, 57(5), 397-398, 1976.
LET95: C. Letellier, P. Dutertre & B. Maheu, Unstable periodic orbits and templates of the Rössler system: toward a systematic topological characterization, Chaos: An Interdisciplinary Journal of Nonlinear Science, 5(1), 271-282, 1995.
CHE99: G. Chen & T. Ueta, Yet another chaotic attractor, International Journal of Bifurcation and Chaos, 9(07), 1465-1466, 1999.
ROS15: M. Rosalie & C. Letellier Systematic template extraction from chaotic attractors: II. Genus-one attractors with multiple unimodal folding mechanisms, Journal of Physics A: Mathematical and Theoretical, 48 (23), 235101, 2015.